Teoría del Display de 7 segmentos de ánodo común.(trabajo final tecnologia)

Teoría del Display de 7 segmentos de ánodo común

El display 7 Segmentos es un dispositivo opto-electrónico que permite visualizar números del 0 al 9. Existen dos tipos de display, de cátodo común y de ánodo común. Este tipo de elemento de salida digital o display, se utilizabá en los primeros dispositivos electrónicos de la década de los 70’s y 80’s. Hoy en día es muy utilizadon en proyectos educativos o en sistemas vintage. También debido a su facilidad de uso, mantenimiento y costo, son utilizados en relojes gigantes o incluso como marcadores en algunos tipos de canchas deportivas.

Es importante mencionar que los display de 7 segmentos, dado que están construidos con diodos LED, requieren una corriente máxima. En otras palabras se requiere colocar una resistencia para limitar la corriente. Dicha resistencia depende de la corriente que se quiera suministrar al LED así como de la caída de voltaje. Para calcular la resistencia usamos la Ley de Ohm. Pueden ver este tutorial para calcular la resistencia de un led. También te puede interesar el código de colores para resistencias.

SÍMBOLO DEL DISPLAY DE 7 SEGMENTOS

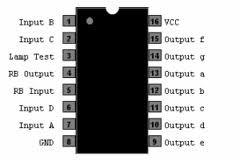
El display de 7 segmentos tiene una estructura casi estándar en cuanto al nombre de los segmentos. Para dicho elemento, se cuenta con 7 leds, uno para cada segmento. Para cada segmento, se le asigna una letra desde la «a» hasta la «g».  El display tiene por nombre a cada uno de los siguientes segmentos, es decir, el símbolo del display 7 segmentos es:

riopos de display de anodo comun
Existen dos tipos principales para los display 7 segmentos. Esta diferencia depende principalmente del arreglo como están conectados los leds que forman a cada segmento. Sabemos que un led tiene dos terminales que se denominan: cátodo y ánodo. El ánodo es la parte positiva del LED, mientras que el cátodo es el pin negativo. Entonces los tipos de display de 7 segmentos se dividen en aquellos de cátodo común y los de ánodo común. Entonces el display tendrá además de los 7 segmentos, 1 pin común. Este pin común se conecta al catodo o al anodo dependiendo del tipo de display.

Teoría del CI 74LS47 (trabajo final tecnologia)

Teoría del CI 74LS47

El  74LS47N es un decodificador/controlador de BCD a siete segmentos con salidas de activación en bajo, diseñadas para la conducción directa de indicadores incandescentes o LEDs de ánodo común. El circuito puede impulsar bujías de lámpara o LEDs de cátodo común. Todos los circuitos, excepto el LS49, tienen controles de entrada/salida de supresión de cresta completa y una entrada para prueba de lámpara. Los patrones de visualización para los contadores de entrada BCD superiores a 9 son símbolos únicos para autenticar las condiciones de entrada. Sus circuitos incorporan control de puesta a cero de flanco positivo o negativo automático (RBI\ y RBO\). La prueba de lámpara (LT/) de estos tipos se puede realizar en cualquier momento cuando el nodo BI\/RBO\ está en nivel alto. Todos los tipos (incluyendo el '49 y el 'LS49) contienen una entrada de borrado (BI\) que puede ser utilizada para controlar la intensidad de la lámpara pulsando o inhibiendo las salidas.

• Salida de colector abierto
• Anodo común
• Las salidas de colector abierto conducen directamente los indicadores
• Provisto con prueba de lámpara
• Puesta a cero con flanco positivo/negativo
• Todos los tipos de circuitos incluyen la capacidad de modulación de intensidad de la lámpara
• Supresión de cero / arrastre de cero
• Todos los tipos de circuitos cuentan con capacidad de modulación de intensidad de lámpara
• Conduce un LED ánodo común mediante indicadores incandescentes
• Disposición de la prueba de la lámpara
• Líder / Supresión cero final
• Todos los tipos de circuitos de características lámpara capacidad de modulación de intensidad
• Salida de Colector Abierto
• Aplicaciones: Procesado de Señal, Defensa, Militar y Aeroespacial  

Código BCD a decimal (trabajo final tecnología)

Código BCD a decimal

Para poder compartir información, que está en formato digital, es común utilizar las representaciones binaria y hexadecimal. Hay otros métodos de representar información y una de ellas es el código BCD o Decimal codificado en binario. Con ayuda de este código es más fácil ver la relación que hay  entre un número decimal (base 10) y el número correspondiente en binario (base 2)Este código utiliza 4 dígitos binarios para representar un dígito decimal (0 al 9) (ver en los dos ejemplos que siguen), sin embargo cuando se hace conversión de binario a decimal típica no hay una directa relación entre el dígito decimal y el dígito binario.

Ejemplos de conversión de Decimal a código BCD

Ejemplo 1: La conversión directa típica del número decimal 85 a binario es: 8510 = 10101012.

La representación del mismo número decimal en BCD se muestra en la siguiente imagen.

Ejemplo 2: La conversión directa típica del número decimal 568 a binario es: 56810 = 10001110002.

La representación del mismo número decimal en BCD se muestra a la siguiente imagen.

Como se puede ver, de los dos ejemplos anteriores, la representación del número en binario no se parece a la representación final en BCD.

¿Cómo obtener el código BCD de cada cifra?

Para poder obtener el equivalente BCD de cada cifra de los números anteriores, se asigna un “peso” o “valor” según la posición que ocupa. Este “peso” o “valor” sigue el siguiente orden: 8 – 4 – 2 – 1. (Es un código ponderado). Del último ejemplo se observa que el número 5 se representa como: 0 1 0 1.

El primer “0” corresponde al 8, el primer “1” corresponde a 4, el segundo “0” corresponde a 2, y… el segundo “1” corresponde a 1. De lo anterior: 0 x 8 + 1 x 4 + 0 x 2 + 1 x 1 = 5

Al código BCD que tiene los “pesos” o “valores” antes descritos se le llama: Código BCD natural. Este código cuenta como un número binario normal del 0 al 9, pero del diez (1010) al quince (1111) no son permitidos pues no existen, para estos números el equivalente de una cifra en decimal.

Aplicaciones

Este código tiene muy pocas aplicaciones. La mas conocida y evidente es la representación de las cifras de los números decimales en displays de 7 segmentos.

Notas: Los subíndices 2 y 10, se utilizan para acotar, en el primer caso que el número es binario y en el segundo caso, que el número es decimal.